The mechanical poetry of semantic embeddings
Paris - France + Germany = Berlin
This bizarre equation is a genuine result from a natural language processing technique that represents words as vectors of numbers. In this post we apply this tool to an analogical reasoning problem, then go on to explore some possible applications.
Words as vectors of numbers
Word “embeddings” are numerical representations of words or phrases. They are created by a machine-learning process that seeks to predict the probability of a certain word occurring given the context of other co-occurring words. Thus the vectors embed a representation of the contexts in which a word arises. This means they also encode semantic and syntactic patterns. It works a bit like a form of compression. Instead of words being arbitrarily long sequences of letters, they become fixed-length sequences of decimal numbers.
The vectors themselves are just sequences of numbers. They don’t mean a lot in isolation, much like a single word in a foreign language written in an exotic alphabet. Having more words (vectors) helps - each provides context for the others. We can start to combine and compare words by doing linear algebra on the vectors. This provides a fascinating insight into the relationships between words. Comparisons also allow us to interpret the vectors in natural language terms (to extend the above metaphor - this is like having a translator for that foreign alphabet).
We can explore this a little with visualisation. It is practically impossible to display vectors with e.g. 300 dimensions graphically in a way the human eye can interpret, but there are techniques available to compress high dimensional vectors so that we can visualise a more-or-less faithful representation of them in 2-dimensional space. The t-SNE (t-Distributed Stochastic Neighbour Embedding) algorithm is one such approach that is designed to preserve the local structure of the network - arranging the vectors according to how neighbours relate to one another.
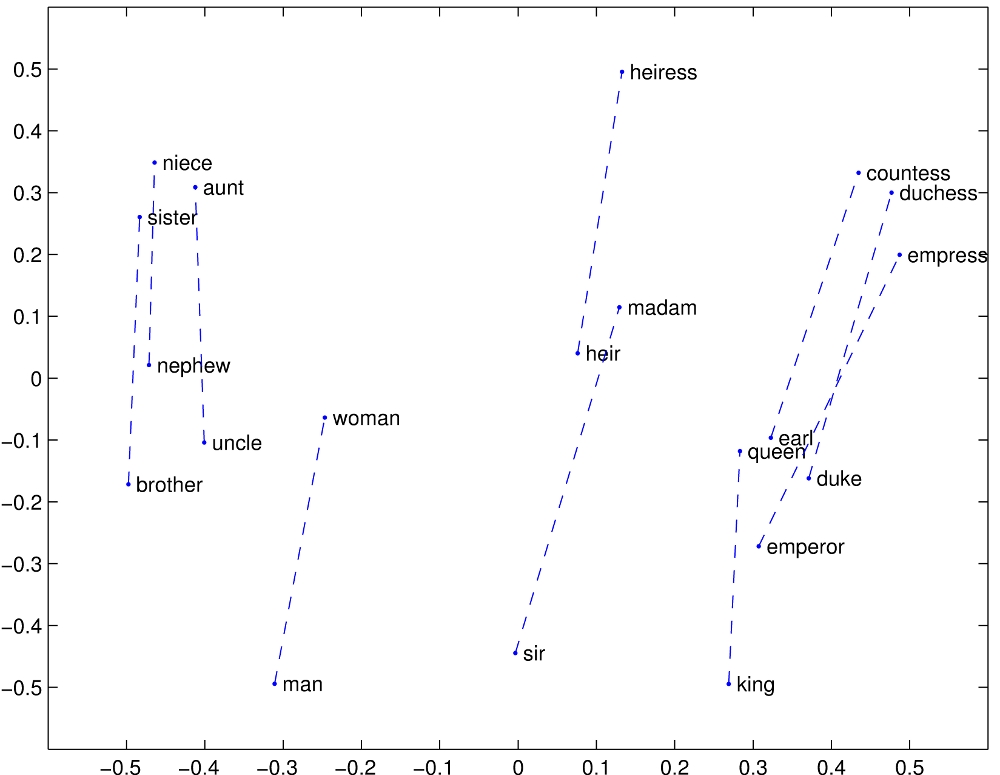
This example, from Pennington, Socher, Manning (2014) Global Vectors for Word Representation, shows comparisons of the vectors for pairs of words. On the below diagram, each word vector is displayed as a point in the 2d space, the comparison between pairs of words is displayed as a dotted-blue line. The vector difference between man - woman, king - queen, and brother - sister all seem broadly similar (in terms of length and orientation). This suggests there is a common structure that represents the semantic distinction between these two genders.
By combining the vectors of several words, we can calculate new aggregate vectors (using vector addition and subtraction from linear algebra):
Paris - France + Germany = ?
We can take the vector that represents Paris then subtract the one that represents France and instead add in the vector for Germany. The resulting vector that we calculate (represented with the ? in the equation above) represents something like “Germany’s equivalent of France’s Paris”. These transformation don’t produce vectors that correspond to other words exactly but we can look for the word with the closest match (the distance can be measured with cosine-similarity - the angle that separates the vectors). In this case the result is Berlin!
Another way of describing these “equations” is to use the semantics of analogy: “Paris is to France as Berlin is to Germany”. There’s a ratio notation for analogies like this:
France : Paris :: Germany : Berlin
These analogies are used to test mental ability. In the US, the Miller Analogies Test is used to assess candidates for post graduate education. The student is presented with a partial analogy - one in which a term is removed - and then asked to fill-in the blanks.
Can we use word embeddings to respond to a Miller Analogies Test?
Analogical reasoning with word embeddings
The Miller Analogies test presents a partial analogy:
Shard : Pottery :: ? : Wood
And a set of 4 options:
acornsmokechairsplinter
You need to choose the one which best completes the analogy. In this case, splinter is the correct answer.
We can think of the analogies A : B :: C : D working like a mathematical formula: A - B = C - D. This equation may be rearranged to solve for the missing element. This gives us an expression which we can use to calculate a new vector that represents the blanked-out term in the analogy. The resulting vector is then compared against the multiple-choice options to find the option that most closely resembles the analogical “idea” that results from the embeddings.
We can visualise this for the splinter example. We take the vector differnce shard - pottery (dashed blue line) then add that to wood to yield a vector for the missing term ?. We then choose the nearest option (choices in green).
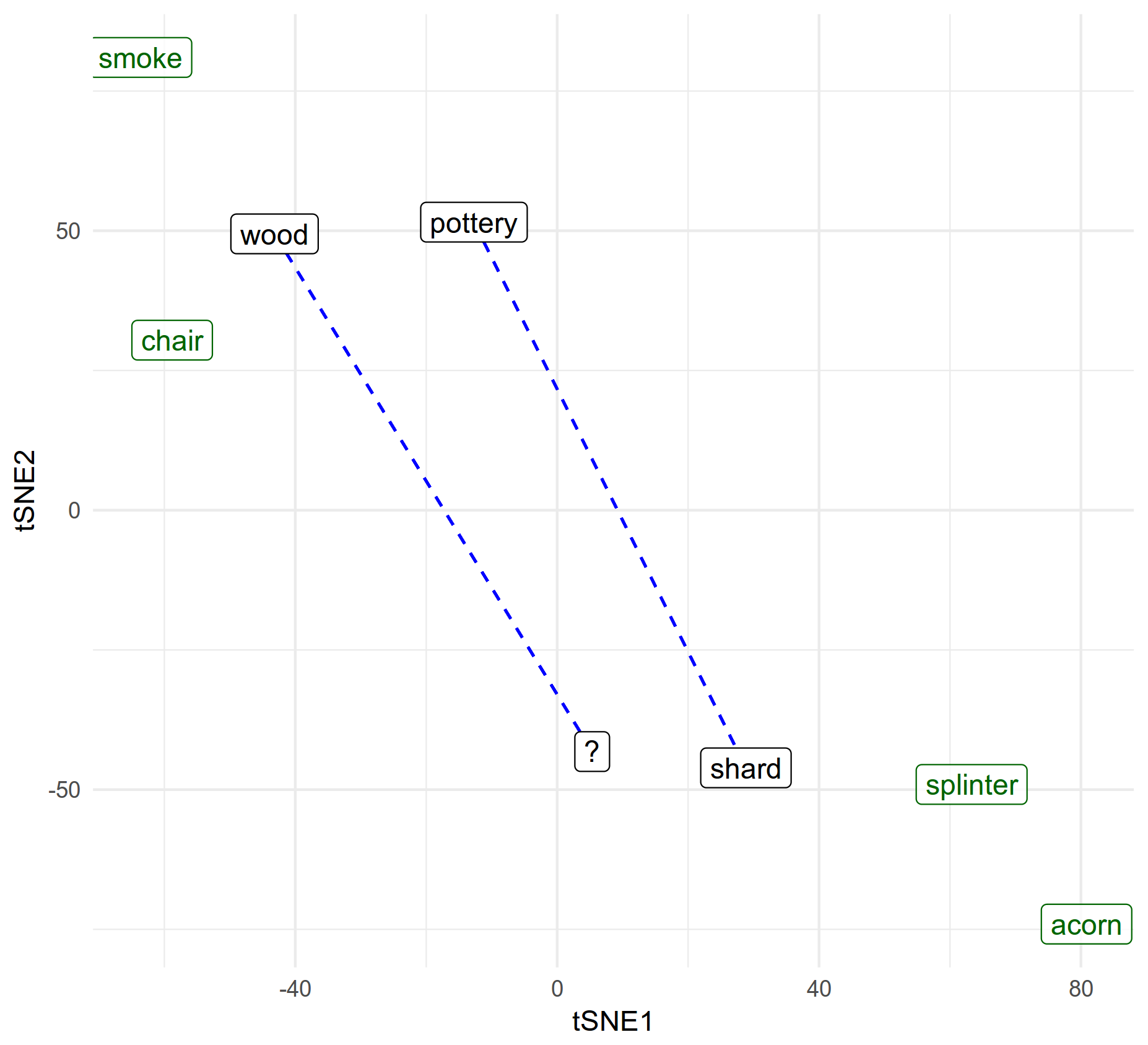
Note that the nearness is measured with cosine-similarity so it’s not exactly the same as 2d euclidian difference as suggested by the plot (although it ought to be broadly equivalent). Indeed proximity doesn’t necessarily mean anything in t-SNE visualisations. The plot is presented to help explain how we’re solving the partial analogies. The distill journal (which provides excellent visual explanations of machine-learning) has some insightful guidance on configuring and interpreting tsne effectively. In this case the plot is quite contrived - it only includes the 8 terms we’re interested in, and I generated several random variations until I found one that best demonstrated the overall shape that illustrates the idea.
The t-SNE visualisation was prepared in R using the Rtsne package (which wraps the original C++ implementation and is much faster than the pure R tsne version) and the mighty ggplot2.
Putting the theory to the test
I implemented this partial-analogy solving algorithm using the Deep Learning for Java library to ingest and analyse the GloVe data and a handful of Clojure functions to tie all the linear algebra together.
I then applied the algorithm to some Miller Analogy tests taken from this example set with the kind permission of majortests.com. I had to remove a couple of questions that didn’t use terms present in the vocabulary of the model - e.g. “Sri Lanka” is actually two words and “-ful” etc are suffixes not words.
This approach leads to 9 correct answers of a possible 13 - a 70% success rate. This is far better than the 25% score we would get from responding at random and is even better than the 55% average score for humans reported by majortests.com.
Which then does it get wrong?
An incorrect answer was given to the question which asks about numbers:
17 : 19 :: ? : 37
The options presented were: 39, 36, 34 and 31. The algorithm picked 39 while the correct answer was 31 - the question is looking for consecutive pairs of primes. As insightful as the word embeddings are, we wouldn’t have expected the co-incidence of numbers in text (which the embeddings capture) to tell us anything about mathematical properties of those numbers, primes or otherwise (expect perhaps something like Benford’s Law which describes the relative incidence of numbers!).
It’s tempting to think of these calculations we do with word embeddings as logical equations. But there’s no mathematical reasoning or understanding of physical cause and effect here. Some results taken from the GloVe dataset again:
Five - One + Two = Four
Fire - Oxygen + Water = Fires
Another incorrect answer was given to this question:
? : puccini :: sculpture : opera
The options presented were: Cellini, Rembrandt, Wagner, and Petrarch. The algorithm suggests Petrarch whereas the correct answer was Cellini. Ultimately the equation here becomes Puccini - Opera + Sculpture. It’s hard to say where things went wrong but I wonder if Cellini was penalised as there is an opera named after him - leaving Petrarch as the only Italian. Reversing the relation (Cellini - Sculpture + Opera) results in vector very close to Puccini.
This leaves the following partial analogy that we might otherwise have expected the word embeddings to solve correctly:
Penury : Money :: Starvation : ?
The options presented were: Sustenance, Infirmity, Illness and Care. The algorithm suggests Care is the best fit, whereas we are expecting Sustenance; as explained by millertests.com, penury is the result of having no money, starvation is the result of having no food. The closest words found by the algorithm (i.e. an open answer, not those options specified in the test) are in the topic area we’d expect: overwork, malnutrition and famines.
The Oxford English Dictionary defines two meanings of Penury: the first is poverty, and the second is scarcity. Similarly Sustenance can refer to a livelihood as well as food. If we replace Penury with Poverty or Sustenance with Food the same algorithm finds the correct answer. This suggests that the multiple meanings are introducing some ambiguity. Curiously these replacements aren’t in the list of 10 words closest to the words we’re substituting them for - there is a substantive distinction to be made.
I think this example serves as a useful reminder that this approach is naively mechanistic. The human reader will automatically distinguish the appropriate meaning by re-appraising the context - the context of starvation means the nutrition-interpretation of sustenance comes to mind much more readily. Perhaps the algorithm could be further improved by doing something similar… We can use the idea of “Dog” to distinguish between “Cat as in Pet” and “Cat as in CAT scan”:
Cat - Dog = Tomography
Applications of word-embeddings
As we’ve seen above the vectors give a numerical value for the similarity of words. A simple use would be to expand search requests using synonyms and associations or even to automatically generate a thesaurus. This would be much more powerful than a keyword search as a measure of the proximity of meaning is encoded - i.e. not literally the word you searched for but also related terms, you could even make distinctions like “please find documents about cat as in scan, not as in pet”.
Compound vectors built-up from word embeddings can be used to represent larger structures too - like sentences or whole documents. These can be used to define the sentiment of a sentence or topic of a document. They could also help to identify documents that are related to a given topic (or corpus) for grouping or retrieval. You don’t necessarily need to identify the topic by name (or a collection of names) - the topic is identified by an abstract vector of numbers - so you can start with a seed document or corpus and request some suggestions of other related ones.
From retrieval we can extend further into discovery. Swanson linking is the idea of discovering new relationships by finding connections between existing (but separate) knowledge. This is not about finding new knowledge, but a process through which we can find lessons from one area and apply them to another.
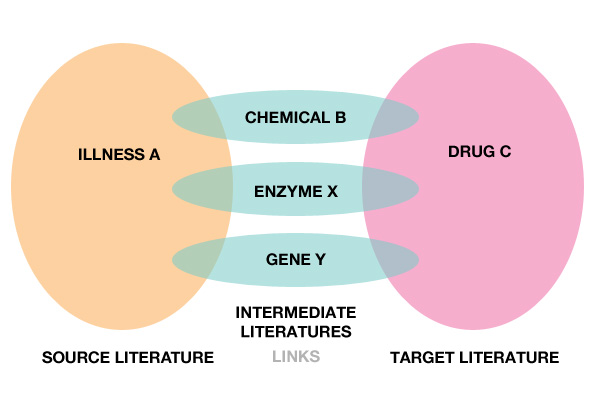
By Robin Davis - Own work, CC BY-SA 3.0, Link
More curiously this can also be extended to machine translation or the expansion of bilingual dictionaries. To achieve this feat, the embeddings are initialised using existing translations (“word alignments”) and then further trained monolingually (so they capture word context) or bilingually (so they optimise for between-language translational equivalence as well as learning within-language context). Similarities in semantic structures between two languages can become apparent once they are mapped onto the same feature space. This provides insight into new translations and incidentally makes for a novel way to explore alternative interpretations.
Perhaps the most powerful prospect of word-embeddings through, is their potential for application in other algorithms that need a base representation of language. An important task in natural-language processing, for example, is that of named-entity recognition (i.e. being able to spot the names of people, companies or places in documents). It has been shown that word embeddings can be used as a feature (i.e. way of describing the input text) when training such systems, leading to improved accuracy.
Finally, although it’s not really a practical application, I’ve been quite entertained playing with these vectors. There is a dense network of meaning deep within the numbers. Of course many of the results are prosaic but others are very pleasing. There is only as much imagination present as you put in - the process is entirely mechanical after all - but the outputs can be surprisingly expressive…
life - death + stone = bricks
productivity - economic + social = absenteeism
word - mechanism + creativity = poetry
poetry - words + sound = music
home - house + building = stadium
trust + money - banking = charitable
lifestyle + happy - sad = habits
habit + happy - sad = eating
eating + happy - sad = vegetarian
ship - water + earth = spacecraft
power - energy + money = bribes